Softmax with cross-entropy

Posted on June 25, 2017

backpropogation, matrix calculus, softmax, cross-entropy, neural networks, deep learning

A matrix-calculus approach to deriving the sensitivity of cross-entropy cost to the weighted input to a softmax output layer. We use row vectors and row gradients, since typical neural network formulations let columns correspond to features, and rows correspond to examples. This means that the input to our softmax layer is a row vector with a column for each class.

Softmax

Softmax is a vector-to-vector transformation that turns a row vector

$\mathbf x = \begin{bmatrix} x_1 \ \, x_2 \ \, ... \ \, x_n \end{bmatrix}$

into a normalized row vector

$\mathbf s(\mathbf x) = \begin{bmatrix} s(\mathbf x)_1 \ \, s(\mathbf x)_2 \ \, ... \ \, s(\mathbf x)_n \end{bmatrix}$

The transformation is easiest to describe element-wise. The $i$ th output $s(\mathbf x)_i$ is a function of the entire input $\mathbf x$ , and is given by

$s(\mathbf x)_i = \frac{e^{x_i}}{\sum e^{x_j}}$

Softmax is nice because it turns $\mathbf x$ into a probability distribution.

Each element $s(\mathbf x)_i$ is between $0$ and $1$ .
The elements $s(\mathbf x)_i$ sum to $1$ .

Invariance to scaling

Softmax is invariant to additively scaling $\mathbf x$ by a constant $c$ .

$\begin{aligned} s(\mathbf x + c)_i &= \frac{e^{x_i + c}}{\sum e^{x_j + c}} \\[1.6em] &= \frac{e^{x_i}e^c}{\sum e^{x_j}e^c} \\[1.6em] &= \frac{e^{x_i}}{\sum e^{x_j}} \end{aligned}$

In other words, softmax only cares about the relative differences in the elements of $\mathbf x$ . That means we can protect softmax from overflow by subtracting the maximum element of $\mathbf x$ from every element of $\mathbf x$ . This will also protect against underflow because the denominator will contain a sum of non-negative terms, one of which is $e^{x_\text{max} - x_\text{max}} = 1$ .

Softmax in Python

def softmax(x):
    """Return the softmax of a vector x.
    
    :type x: ndarray
    :param x: vector input
    
    :returns: ndarray of same length as x
    """
    x = x - np.max(x)
    row_sum = np.sum(np.exp(x))
    return np.array([np.exp(x_i) / row_sum for x_i in x])

Jacobian of softmax

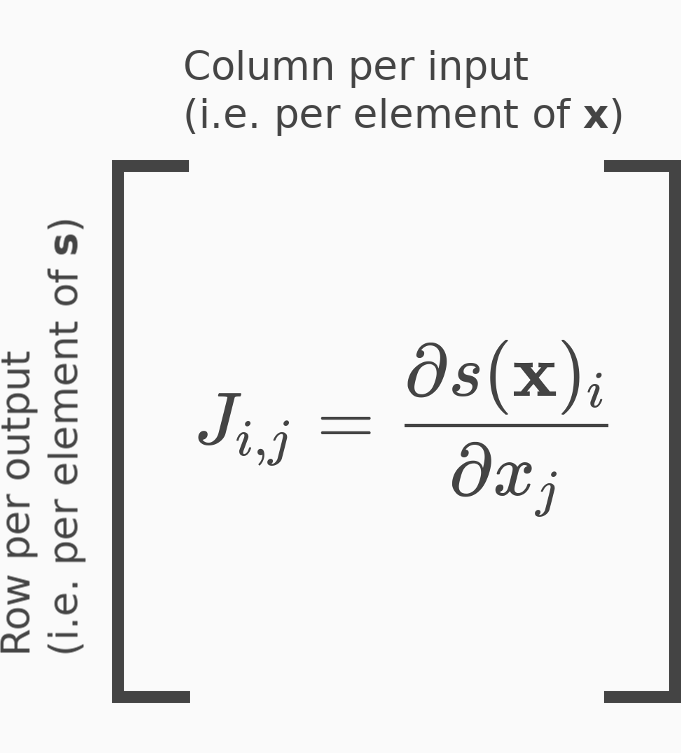
Since softmax is a vector-to-vector transformation, its derivative is a Jacobian matrix. The Jacobian has a row for each output element $s_i$ , and a column for each input element $x_j$ .

The entries of the Jacobian take two forms, one for the main diagonal entry, and one for every off-diagonal entry. We’ll show how to compute these entries for an arbitrary row $i$ of the Jacobian.

Diagonal row entry

First compute the diagonal entry of row $i$ . That is, compute the derivative of the $i$ ‘th output, $s_i$ , with respect to its $i$ ‘th input, $x_i$ . All we need is the division rule from calculus.

$\begin{aligned} \frac{\partial s(\mathbf x)_i}{\partial x_i} &= \frac{\sum_j e^{x_j} e^{x_i} - e^{x_i} e^{x_i}}{(\sum_j e^{x_j})^2} \\[1.6em] &= s(\mathbf x)_i - s(\mathbf x)_i^2 \end{aligned}$

Off-diagonal row entries

Now compute every off-diagonal entry of row $i$ . That is, compute the derivative of the $i$ ‘th output, $s_i$ , with respect to its $j$ ‘th input, $x_j$ , where $j \neq i$ . Again we use the division rule, but in this case the derivative of the numerator, $e^{x_i}$ with respect to $x_j$ is zero, because $j \neq i$ means the numerator is constant with respect to $x_j$ .

$\begin{aligned} \frac{\partial s(\mathbf x)_i}{\partial x_j} &= \frac{\sum_j e^{x_j} \cdot 0 - e^{x_i} e^{x_j}}{(\sum_j e^{x_j})^2} \\[1.6em] &= - s(\mathbf x)_i s(\mathbf x)_j \end{aligned}$

This is nice! The derivative of softmax is always phrased in terms of softmax.

From now on, to keep things clear, we won’t write dependence on $\mathbf x$ . Instead we’ll write $\mathbf s(\mathbf x)$ as $\mathbf s$ and $s(\mathbf x)_i$ as $s_i$ , understanding that $\mathbf s$ and $s_i$ are each a function of the entire vector $\mathbf x$ .

Full Jacobian

The form of the off-diagonals tells us that the Jacobian of softmax is a symmetric matrix. This is nice because symmetric matrices have great numeric and analytic properties. We expand it below. Each row is a gradient of one output element $s_i$ with respect to each of its input elements $x_j$ .

$\mathbf J_{\mathbf x}(\mathbf s) = \begin{bmatrix} s_0 - s_0^2 & -s_0 s_1 & ... & -s_0 s_n \\[0.6em] -s_1 s_0 & s_1 - s_1^2 & ... & -s_1 s_n \\[0.6em] ... & ... & ... & ... \\[0.6em] -s_n s_0 & -s_n s_1 & ... & s_n - s_n^2 \end{bmatrix}$

Notice that we can express this matrix as

$\mathbf J_{\mathbf x}(\mathbf s) = \text{diag}(\mathbf s) - \mathbf s^\top \mathbf s$

where the second term is the $n \times n$ outer product, because we defined $\mathbf s$ as a row vector.

Jacobian of softmax in Python

def jacobian_softmax(s):
    """Return the Jacobian matrix of softmax vector s.

    :type s: ndarray
    :param s: vector input

    :returns: ndarray of shape (len(s), len(s))
    """
    return np.diag(s) - np.outer(s, s)

Cross-entropy

Cross-entropy measures the difference between two probability distributions. We saw that $\mathbf s$ is a distribution. The correct class is also a distribution if we encode it as a one-hot vector:

$\begin{aligned} \mathbf y &= \begin{bmatrix} y_1 \ \, y_2 \ \, ... \ \, y_n \end{bmatrix} \\[1.1em] &= \begin{bmatrix} 0 \ \ \, 0 \ \ \, ... \ \ \, 1 \ \ \, ... \ \ \, 0 \end{bmatrix} \end{aligned}$

where the $1$ appears at the index of the correct class of this single example.

The cross-entropy between our predicted distribution over classes, $\mathbf s$ , and the true distribution over classes, $\mathbf y$ , is a scalar measure of their difference, which is perfect for a cost function. It’ll drive our softmax distribution toward the one-hot distribution. We can write this cost function as

$\begin{aligned} H(\mathbf y, \mathbf s) &= -\sum_{i=1}^n y_i \log s_i \\[1.6em] &= -\mathbf y \log \mathbf s^\top \end{aligned}$

which is the dot product since we’re using row vectors. This formula comes from information theory. It measures the information gained about our softmax distribution when we sample from our one-hot distribution.

Cross-entropy in Python

def cross_entropy(y, s):
    """Return the cross-entropy of vectors y and s.

    :type y: ndarray
    :param y: one-hot vector encoding correct class

    :type s: ndarray
    :param s: softmax vector

    :returns: scalar cost
    """
    # Naively computes log(s_i) even when y_i = 0
    # return -y.dot(np.log(s))
    
    # Efficient, but assumes y is one-hot
    return -np.log(s[np.where(y)])

Gradient of cross-entropy

Since our $\mathbf y$ is given and fixed, cross-entropy is a vector-to-scalar function of only our softmax distribution. That means it will have a gradient with respect to our softmax distribution. This vector-to-scalar cost function is actually made up of two steps: (1) a vector-to-vector element-wise $\log$ and (2) a vector-to-scalar dot product. The vector-to-vector logarithm will have a Jacobian, but since it’s applied element-wise, the Jacobian will be diagonal, holding each elementwise derivative. The gradient of a dot product, being a linear operation, is just the vector $\mathbf y$ .

$\begin{aligned} \nabla_{\mathbf s} H &= -\nabla_{\mathbf s} \mathbf y \log \mathbf s^\top \\[1.6em] &= -\mathbf y \nabla_{\mathbf s} \log \mathbf s \\[1.1em] &= -\mathbf y \ \text{diag}\left(\frac{\mathbf 1}{\mathbf s}\right) \\[1.6em] &= -\frac{\mathbf y}{\mathbf s} \end{aligned}$

where we used equation (69) of the matrix cookbook for the derivative of the dot product.

Gradient of cross-entropy in Python

def gradient_cross_entropy(y, s):
    """Return the gradient of cross-entropy of vectors y and s.

    :type y: ndarray
    :param y: one-hot vector encoding correct class

    :type s: ndarray
    :param s: softmax vector

    :returns: ndarray of size len(s)
    """
    return -y / s

Error at input to softmax layer

By the chain rule, the sensitivity of cost $H$ to the input to the softmax layer, $\mathbf x$ , is given by a gradient-Jacobian product, each of which we’ve already computed:

$\nabla_{\mathbf x} H = \nabla_{\mathbf s} H \ \mathbf J_{\mathbf x}(\mathbf s)$

The first term is the gradient of cross-entropy to softmax activation. The second term is the Jacobian of softmax activation to softmax input. Remember that we’re using row gradients - so this is a row vector times a matrix, resulting in a row vector. Expanding and simplifying, we get

$\begin{aligned} \nabla_{\mathbf x} H &= -\frac{\mathbf y}{\mathbf s} \bigg[\text{diag}(\mathbf s) -\mathbf s^\top \mathbf s \bigg] \\[1.6em] &= \frac{\mathbf y}{\mathbf s} \mathbf s^\top \mathbf s - \frac{\mathbf y}{\mathbf s} \ \text{diag}(\mathbf s) \\[1.6em] &= \mathbf y \ \mathbf S^{\text{repeated row}} - \mathbf y \\[1.6em] &= \mathbf s - \mathbf y \end{aligned}$

The last line follows from the fact that $\mathbf y$ was one-hot and applied to a matrix whose rows are identically our softmax distribution. But actually, any $\mathbf y$ whose elements sum to $1$ would satisfy the same property. To be more specific, the equation above would hold not just for one-hot $\mathbf y$ , but for any $\mathbf y$ specifying a distribution over classes.

Error at input to softmax layer in Python

def error_softmax_input(y, s):
    """Return the sensitivity of cross-entropy cost to input of softmax.

    :type y: ndarray
    :param y: one-hot vector encoding correct class

    :type s: ndarray
    :param s: softmax vector

    :returns: ndarray of size len(s)
    """
    return s - y

Now with a batch of examples

Our work thus far considered a single example. Hence $\mathbf x$ , our input to the softmax layer, was a row vector. Alternatively, if we feed forward a batch of $m$ examples, then $\mathbf X$ contains a row vector for each example in the minibatch.

$\mathbf X = \begin{bmatrix} \mathbf x_1 \\[0.6em] \mathbf x_2 \\[0.6em] ... \\[0.6em] \mathbf x_m \end{bmatrix} \sim m \times n$

Batch softmax

Softmax is still a vector-to-vector transformation, but it’s applied independently to each row of $\mathbf X$ .

$\mathbf S = \begin{bmatrix} \mathbf s(\mathbf x_1) \\[0.6em] \mathbf s(\mathbf x_2) \\[0.6em] ... \\[0.6em] \mathbf s(\mathbf x_m) \end{bmatrix} \sim m \times n$

Batch softmax in Python

def batch_softmax(x):
    """Return matrix of row-wise softmax of x.

    :type x: ndarray
    :param x: row per example and column per feature

    :returns: ndarray of x.shape after row-wise softmax
    """
    # Stabilize by subtracting row max from each row
    row_maxes = np.max(x, axis=1)
    row_maxes = row_maxes[:, np.newaxis]  # for broadcasting
    x = x - row_maxes

    return np.array([softmax(row) for row in x])

Jacobian of batch softmax

Because rows are independently mapped, the Jacobian of row $i$ of $\mathbf S$ with respect to row $j \neq i$ of $\mathbf X$ is a zero matrix.

$\mathbf J_{\mathbf x_{j \neq i}}(\mathbf s_i) = \mathbf 0$

and the Jacobian of row $i$ of $\mathbf S$ with respect to row $i$ of $\mathbf X$ is our familiar matrix from before

$\mathbf J_{\mathbf x_{i}}(\mathbf s_i) = \text{diag}(\mathbf s_i) - \mathbf s_i^\top \mathbf s_i$

That means our grand Jacobian of $\mathbf S$ with respect to $\mathbf X$ is a diagonal $m \times m$ matrix of $n \times n$ matrices, most of which are zero matrices:

$\mathbf J_{\mathbf X}(\mathbf S) = \begin{bmatrix} \mathbf J_{\mathbf x_1}(\mathbf s_1) & \mathbf 0 & ... & \mathbf 0 \\[1.1em] \mathbf 0 & \mathbf J_{\mathbf x_2}(\mathbf s_2) & ... & \mathbf 0 \\[1.1em] ... & ... & ... & ... \\[1.1em] \mathbf 0 & \mathbf 0 & ... & \mathbf J_{\mathbf x_m}(\mathbf s_m) \end{bmatrix}$

Jacobian of batch softmax in Python

def jacobian_batch_softmax(s):
    """Return array of row-wise Jacobians of s.

    :type s: ndarray
    :param s: matrix whose rows are softmaxed

    :returns: ndarray of shape
              (s.shape[0], s.shape[0], s.shape[1], s.shape[1])
    """
    # Array of nonzero Jacobians lying along tensor diagonal
    return np.array([jacobian_softmax(row) for row in s])

Mean cross-entropy of batch

Let each row of $\mathbf Y$ be a one-hot label for an example:

$\mathbf Y = \begin{bmatrix} \mathbf y_1 \\[0.6em] \mathbf y_2 \\[0.6em] ... \\[0.6em] \mathbf y_m \end{bmatrix} \sim m \times n$

Then we compute the mean cross-entropy by averaging the cross-entropy of every matching pair of rows of $\mathbf Y$ and $\mathbf S$ . That is, we average over examples, the cross-entropy of each example:

$\begin{aligned} H(\mathbf Y, \mathbf S) &= -\frac{1}{m} \sum_{i=1}^m \mathbf y_i \log \mathbf s_i^\top \\[1.6em] &= -\frac{1}{m} \text{Tr}(\mathbf Y \log \mathbf S^\top) \end{aligned}$

The above simplification works because each row of $\mathbf S$ is $\mathbf s_i$ . So each column of $\mathbf S^\top$ is $\mathbf s_i$ . So the matrix product $\mathbf Y \log \mathbf S^\top$ dots rows of $\mathbf Y$ with columns of $(\log \mathbf S^\top)$ , which is exactly what we want for cross-entropy. Now, we only care about entries where the row index equals the column index. That’s because cross-entropy sums the dot products of matching rows of $\mathbf Y$ and $\mathbf S$ . We can sum over matching dot products by using a trace.

Note: this formulation is computationally wasteful. We shouldn’t implement batch cross-entropy this way in a computer. We’re only using it for its analytic simplicity to work out the backpropogating error. However, the end analytic result is actually computationally efficient.

Mean cross-entropy of batch in Python

def mean_cross_entropy(y, s):
    """Return the mean row-wise cross-entropy of y and s.

    :type y: ndarray
    :param y: matrix whose rows are one-hot vectors encoding
              the correct class of each example.

    :type s: ndarray
    :param s: matrix whose every row is a softmax distribution over
              class predictions for a given example.

    :returns: scalar, mean row-wise cross-entropy cost
    """
    return np.mean([cross_entropy(y_row, s_row)
                    for y_row, s_row in zip(y, s)])

Jacobian of mean cross-entropy of batch

Since mean cross-entropy maps a matrix to a scalar, its Jacobian with respect to $\mathbf S$ will be a matrix.

$\begin{aligned} \mathbf J_{\mathbf S}(H) &= -\mathbf J_{\mathbf S} \bigg(\frac{1}{m} \text{Tr}(\mathbf Y \log \mathbf S^\top) \bigg) \\[1.6em] &= -\frac{1}{m} \mathbf J_{\mathbf S} \text{Tr}(\mathbf Y \log \mathbf S^\top) \\[1.6em] &= -\frac{1}{m} \mathbf Y \mathbf J_{\mathbf S} \log \mathbf S \\[1.6em] &= -\frac{1}{m} \mathbf Y \odot \frac{1}{\mathbf S} \\[1.6em] &= -\frac{1}{m} \frac{\mathbf Y}{\mathbf S} \end{aligned}$

Since $\log \mathbf S$ is an element-wise operation mapping a matrix to a matrix, its Jacobian is a matrix of element-wise derivatives which we chain rule by a Hadamard product, rather than by a dot product.

Why this works

This procedure is always true for any element-wise operations. We can see this by concatenating the rows of $\mathbf S$ .

$\mathbf s = \begin{bmatrix} \mathbf s_1 \ \, \mathbf s_2 \ \, ... \ \, \mathbf s_m \end{bmatrix}$

such that $\mathbf s$ is a row vector of length $m \cdot n$ . Then $\log$ is an element-wise vector-to-vector transformation again. So it has an $m \cdot n \times m \cdot n$ diagonal Jacobian matrix.

$\mathbf J_{\mathbf s}(\log \mathbf s) = \text{diag}\left(\frac{\mathbf 1}{\mathbf s}\right)$

If we flatten $\mathbf Y$ in the same way

$\mathbf y = \begin{bmatrix} \mathbf y_1 \ \, \mathbf y_2 \ \, ... \ \, \mathbf y_m \end{bmatrix}$

then we get

$H(\mathbf y, \mathbf s) = - \frac{1}{m} \mathbf y \log \mathbf s^\top$

and so

$\begin{aligned} \mathbf J_{\mathbf s}(H) &= -\frac{1}{m} \mathbf y \frac{\partial}{\partial \mathbf s} \Big(\log \mathbf s \Big) \\[1.6em] &= -\frac{1}{m} \mathbf y \text{diag}\left(\frac{\mathbf 1}{\mathbf s}\right) \\[1.6em] &= -\frac{1}{m} \frac{\mathbf y}{\mathbf s} \end{aligned}$

Now since $\mathbf y$ and $\mathbf s$ are each of length $m \cdot n$ , we can reshape this formulation back into matrices, understanding that in both cases the division is element-wise:

$\mathbf J_{\mathbf s}(H) = -\frac{1}{m} \frac{\mathbf Y}{\mathbf S}$

and we have our result. $\square$

Jacobian of mean cross-entropy of batch in Python

def jacobian_mean_cross_entropy(y, s):
    """Return the Jacobian matrix for mean cross-entropy.

    :type y: ndarray
    :param y: matrix whose rows are one-hot vectors encoding
              the correct class of each example.

    :type s: ndarray
    :param s: matrix whose every row is a softmax distribution over
              class predictions for a given example.

    :returns: ndarray of shape y.shape holding gradients as rows
    """
    return -(1 / y.shape[0]) * (y / s)

Error at input to softmax layer for batch

We apply the chain rule just as before. The only difference is that our gradient-Jacobian product is now a matrix-tensor product. Multiplying a matrix against a tensor is difficult. One approach is to flatten everything, do a vector-matrix product as before, and then reshape everything, but this is not elegant or intuitive. Instead, we dot rows of $\mathbf J_{\mathbf S}(H)$ , each a gradient of a row-wise cross-entropy, against diagonal elements of $\mathbf J_{\mathbf X}(\mathbf S)$ , each a Jacobian matrix of a row-wise softmax.

We are able to do this because of the fact that $\mathbf J_{\mathbf X}(\mathbf S)$ is diagonal, which breaks the matrix-tensor product into an element-wise dot product of gradients and Jacobians. We owe this entirely to the fact that softmax is a row-to-row transformation, such that its Jacobian tensor is diagonal.

$\begin{aligned} \mathbf J_{\mathbf X}(H) &= \mathbf J_{\mathbf S}(H) \ \mathbf J_{\mathbf X}(\mathbf S) \\[1.6em] &= \bigg(-\frac{1}{m} \frac{\mathbf Y}{\mathbf S}\bigg) \mathbf J_{\mathbf X}(\mathbf S) \\[2.4em] &= \frac{1}{m} \begin{bmatrix} -\mathbf y_1 / \mathbf s_1 \\[0.4em] -\mathbf y_2 / \mathbf s_2 \\[0.4em] ... \\[0.4em] -\mathbf y_m / \mathbf s_m \end{bmatrix} \mathbf J_{\mathbf X}(\mathbf S) \\[2.4em] \\[0.6em] &= \frac{1}{m} \begin{bmatrix} -\frac{\mathbf y_1}{\mathbf s_1} \mathbf J_{\mathbf x_1}(\mathbf s_1) \\[1.4em] -\frac{\mathbf y_2}{\mathbf s_2} \mathbf J_{\mathbf x_2}(\mathbf s_2) \\[1.4em] ... \\[1.4em] -\frac{\mathbf y_m}{\mathbf s_m} \mathbf J_{\mathbf x_m}(\mathbf s_m) \end{bmatrix} \\[1.4em] \\[0.6em] &= \frac{1}{m} \begin{bmatrix} \mathbf s_1 - \mathbf y_1 \\[0.4em] \mathbf s_2 - \mathbf y_2 \\[0.4em] ... \\[0.4em] \mathbf s_m - \mathbf y_m \end{bmatrix} \\[1.4em] \\[0.6em] &= \frac{1}{m} \Big(\mathbf S - \mathbf Y\Big) \end{aligned}$

Where the third step followed by the fact that $J_{\mathbf X}(\mathbf S)$ is diagonal. So the sensitivity of cost to the weighted input to our softmax layer is just the difference of our softmax matrix and our matrix of one-hot labels, where every element is divided by the number of examples in the batch.

Error at input to softmax layer for batch in Python

def batch_error_softmax_input(y, s):
    """Return the sensitivity of cross-entropy cost to input of softmax.

    :type y: ndarray
    :param y: matrix whose rows are one-hot vectors encoding
              the correct class of each example.

    :type s: ndarray
    :param s: matrix whose every row is a softmax distribution over
              class predictions for a given example.

    :returns: ndarray of shape y.shape
    """
    return (1 / y.shape[0]) * (S - Y)